| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 추상 팩토리
- Coroutines
- Design Pattern
- material3
- 안드로이드 디자인시스템
- 코틀린멀티플랫폼
- android designsystem
- 빌터패턴
- factory method
- 디자인패턴
- 디자인패턴 #
- Abstract Factory
- 추상팩토리패턴
- 코루틴
- 프로토타입 패턴
- designPattern
- kmp
- 함수형프로그래밍
- Observer Pattern
- kotlin multiplatform
- builderPattern
- PrototypePattern
- 팩토리 메소드
- Kotlin
- Functional Programming
- compose
- define
- 옵저버 패턴
- ㅋㅁ
- 코틀린
- Today
- Total
오늘도 더 나은 코드를 작성하였습니까?
이분탐색(Binary Search) 본문
이진 검색 알고리즘(binary search algorithm)
오름차순으로 정렬된 리스트에서 특정한 값의 위치를 찾는 알고리즘이다.
처음 중간의 값을 임의의 값으로 선택하여, 그 값과 찾고자 하는 값의 크고 작음을 비교하는 방식을 채택하고 있다. 처음 선택한 중앙값이 만약 찾는 값보다 크면 그 값은 새로운 최댓값이 되며, 작으면 그 값은 새로운 최솟값이 된다. 검색 원리상 정렬된 리스트에만 사용할 수 있다는 단점이 있지만, 검색이 반복될 때마다 목표값을 찾을 확률은 두 배가 되므로 속도가 빠르다는 장점이 있다
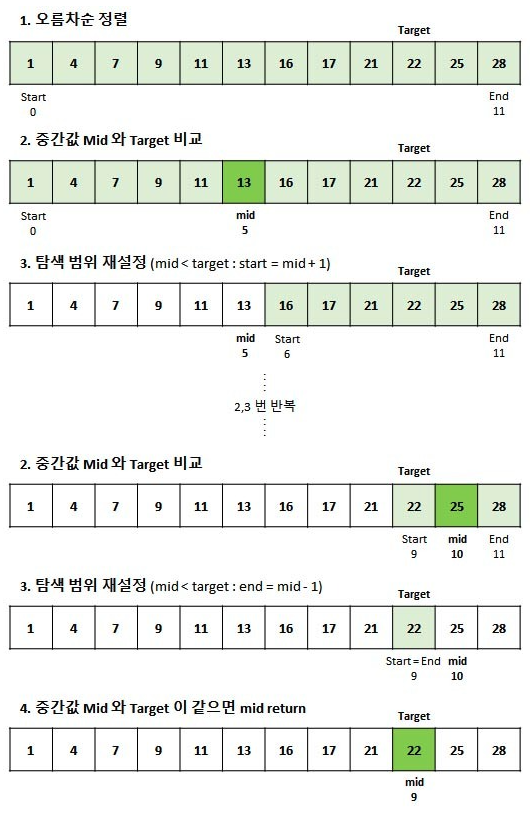
단순히 위의 예제와 구현 코드만 본다면 어렵지 않다.
fun main() {
arr = intArrayOf(1, 4, 7, 9, 11, 13, 16, 17, 21, 22, 25, 28)
val key = 22
var left = 0
var right = arr.lastIndex
while (left <= right) {
val mid = (left + right) / 2
if (arr[mid] == key) {
println(mid)
break
} else if (arr[mid] > key) {
right = mid - 1
} else {
left = mid + 1
}
}
}
예시1) 입국심사.
https://www.acmicpc.net/problem/3079
3079번: 입국심사
첫째 줄에 N과 M이 주어진다. (1 ≤ N ≤ 100,000, 1 ≤ M ≤ 1,000,000,000) 다음 N개 줄에는 각 심사대에서 심사를 하는데 걸리는 시간인 Tk가 주어진다. (1 ≤ Tk ≤ 109)
www.acmicpc.net
M명 N개의 입국 심사대
k번 심사대에 심사 시간 Tk
1 ≤ N ≤ 100_000
1 ≤ M ≤ 1_000_000_000
각 심사대마다 소요 시간(1 ≤ Tk ≤ 10^9)
심사를 마치는데 걸리는 시간의 최솟값
예)
1번 심사대 소요시간 7 - 1 3 5 6
2번 심사대 소요시간 10 - 2 4
7초후 - 1번 완료, 14초후 3번 완료, 21초 후 5번 완료, 28초 후 6번 완료
10초뒤 2번 완료, 20초뒤 4번 완료
문제를 이해하고 예시를 봐도 어떻게 문제를 해결할 수 있을지 감이 오지 않는다.
이때, 비정상적으로 큰 입력값과, 최소값을 결정하는 문제이다. 혹시? 이진 탐색이 아닐까?
무엇을 결정하는가? "모든 인원의 심사시간"
* 이진 탐색 탐색의 결정화 문제는 다루는 숫자가 크기 때문에 가능하면 Long 타입을 사용한다.
left / right를 결정한다.
여기선,
var left: Long = 1 --> (1명, 1개의 검색대 소요시간 1초)
var right: Long = timeArr.maxOrNull()!! * m ( m명, 1개의 검색대 최대 소요시간)
*check() 주어진 심사시간에 모든 인원을 심사할 수 있는지 확인 한다.
심사 가능하다면 -> left --- (mid-1)
심사 불가능하다면 -> (mid+1) --- right
var n = 0
var m = 0L
lateinit var timeArr: Array<Long>
fun check(totalTime: Long): Boolean {
/*
모든 인원을 심사하는데 걸리는 시간을 각 심사대에서 걸리는 시간으로 나눠서
몇 명을 심사 할 수 있는지 카운트
*/
var cnt = 0L
for (i in 0 until timeArr.size) {
cnt += (totalTime / timeArr[i])
if (cnt >= m) return true
}
return false
}
fun main() = with(System.`in`.bufferedReader()) {
val info = readLine().split(" ").map { it.toLong() }
n = info[0].toInt()
m = info[1]
timeArr = Array(n) { readLine().toLong() }
var left: Long = 1
var right: Long = timeArr.maxOrNull()!! * m
var answer = 0L
while (left <= right) {
val mid = (left + right) / 2
if (check(mid)) {
answer = mid
right = mid - 1
} else {
left = mid + 1
}
}
println(answer)
Unit
}
파닭파닭
https://www.acmicpc.net/problem/14627
14627번: 파닭파닭
첫째 줄에 승균이가 시장에서 사 온 파의 개수 S(1 ≤ S ≤ 1,000,000), 그리고 주문받은 파닭의 수 C(1 ≤ C ≤ 1,000,000)가 입력된다. 파의 개수는 항상 파닭의 수를 넘지 않는다. (S ≤ C) 그 후, S 줄에
www.acmicpc.net
시장에서 사 온 파의 개수 S(1 ≤ S ≤ 1,000,000)
주문받은 파닭의 수 C(1 ≤ C ≤ 1,000,000)가 입력된다.
파의 개수는 항상 파닭의 수를 넘지 않는다. (S ≤ C)
파의 길이 L(1 ≤ L ≤ 1,000,000,000)이 정수
길이가 일정하지 않은 파를 구매
각 파닭마다 "일정한" 파량을 넣음
최대한 파를 많이 넣음 --> "최대값"
하나의 파닭에는 하나 이상의 파가 들어가면 안 된다 --> 2개의 파를 섞어서 양을 맞춰서 넣을수 없다는 소리다.
최대로 많이 넣을 파의 양을 결정한다...
*check() 넣을 파의 사이즈면, 지금 만들어야되는 파닭을 만들수 있는지 확인함.
만들 수 있다? -> 더 많이 넣어봄 -> left = mid + 1
만들 수 없다? -> 더 적게 넣어봄 -> right = mid-1
var s: Long = 0
var c: Long = 0
lateinit var parSizeArr: Array<Long>
// 입력된 파의 사이즈면, 각각의 파들로 만들어야 될 파닭을 모두 만들수 있는지 확인.
fun check(size: Long): Boolean {
var cnt: Long = 0
for (i in 0 until parSizeArr.size) {
cnt += parSizeArr[i] / size
}
return cnt >= c
}
fun main() = with(System.`in`.bufferedReader()) {
val info = readLine().split(" ").map { it.toLong() }
s = info[0]
c = info[1]
parSizeArr = Array(s.toInt()) {
readLine().toLong()
}
var left: Long = 1
var right: Long = 1000_000_000L
var maxParSize: Long = 0
while (left <= right) {
val mid = (left + right) / 2L
if (check(mid)) {
maxParSize = mid
left = mid + 1
} else {
right = mid - 1
}
}
// println(maxParSize)
var rest = parSizeArr.sum() - (maxParSize * c)
println(rest)
Unit
}'Algorithm > 개념' 카테고리의 다른 글
| 최단거리 알고리즘 - 다익스트라(dijkstra) feat.kotlin (0) | 2024.03.13 |
|---|---|
| 상한선(upper_bound) & 하한선(lower_bound) feat.kotlin (0) | 2023.11.29 |
| 투포인터(two pointer) (1) | 2023.11.28 |
| 탐욕법(Greedy) (1) | 2023.11.26 |
| 백트레킹(BackTracking) (3) | 2023.11.23 |


