백트레킹(BackTracking)

정의

 

여기서는 일단, 컴퓨터 공학의 알고리즘 문제 해결에 관련한 백트레킹의 개념만 다룹니다.

백트래킹(backtracking)은 한정 조건을 가진 문제를 풀려는 전략이다.

 

백트래킹은 기본적으로 완전탐색을 하는것을 기반으로 합니다.

즉, 가능한 모든 경우를 고려하는것이 첫번째이다. 그리고 각각의 경우의 수를 만족하기 위한 한정적 조건들을 존재합니다.

가능성이 있는 후보를 점진적으로 구축하고 후보가 특정 목표까지 완료될 수 없다고 판단하는 즉시 후보를 포기합니다("backtracking")

 

이때 후보군을 포기할 때 솔루션에 영향을 주는 부분을 변경하였다면,  그것을 반드시 원복 시켜주어야 한다.

이것은 백트래킹뿐 아니라 완전탐색에서도 동일하게 원복시켜주어야 합니다.

https://www.acmicpc.net/problem/9663

9663번: N-Queen

일단 n = 1 인 상황에서 직접 구해보자. 

 

n = 1

1가지

 

 

n = 2

1개의 퀸을 놓는 순간 다른 어느 칸에도 두번째 퀸을 놓을 수가 없음

0가지  

 

 

n = 3

처음부터 시작해서 1개의 퀸을 놓고, 놓지 못하는 위치를 제외하고,

두 번째 퀸의 자리를 찾아서 놓다보면 방법이 없음을 알게된다. 

0가지

 

 

 

 

n = 4

1개씩 퀸을 놓는다고 가정해보면, 일단 각 중복을 포함하여, 퀸마다 놓을수 있는 모든 경우의 수는  16개다

모든 경우 의 수 16 * 16 * 16 * 16 -> 2^16 (65,536)이중에서 서로 공격을 할 수 없는 위치에 있는 경우를 찾아야한다.

즉, 불가능한 경우를 제외하면 된다.

 

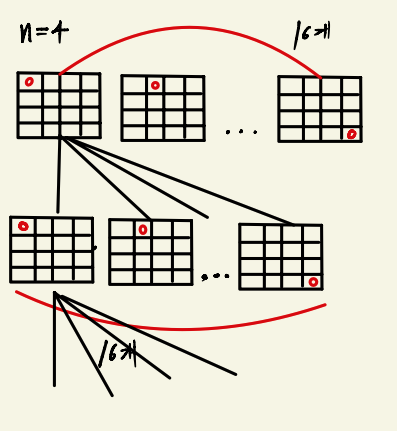
이렇게 하다 보면 중복이 발생하게 된다.

아래 그림을 보면 퀸이 놓인 자리는 동일하지만 놓는 순서가 다르다. 사실상 중복이 발생한다. 

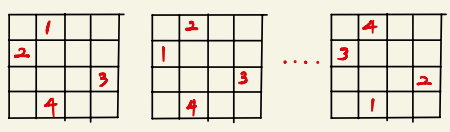
시간 복잡도도 n=8 이면 64*64*64*64*64*64*64*64  2^(64)가까이 되기 때문에 너무 안좋다.

 

여기서 퀸을 놓을때 제한 조건을 생각해보자!

퀸은 가로 세로 대각선을 포함하여 공격이 가능하기 때문에

1행에는 1개의 퀸만 올 수 있다.

그렇다면 모든 경우 의 수 4 * 4 * 4 * 4 -> 2^8로 많이 줄어든다. 

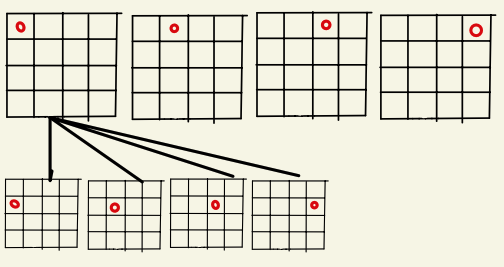
위의 상태에서

1개의 퀸이 놓였을 때 다음 퀸을 놓을수 있는지 없는지 확인할때,

이전의 퀸을 놓을때 열(colum)과 각 대각선 정보를 저장하여, 이미 다른 퀸이 공격 가능한 위치인지 확인한다. 

 

var n = 0

lateinit var map: Array<IntArray>

val points = mutableListOf<Pair<Int, Int>>()

val colSet = HashSet<Int>()

// 왼쪽 위에서 오른쪽 아래 대각방향
val diagonalSet1 = HashSet<Int>()

// 오른쪽 위에서 왼쪽 아래 대각방향
val diagonalSet2 = HashSet<Int>()

var cnt = 0
fun go() {

    // 종료조건
    if (points.size == n) {
        cnt += 1
        return
    }

    var result = 0
    val row = points.size
    for (col in 0 until n) {
        // backtracking
        if (col in colSet) continue
        if (row - col in diagonalSet1) continue
        if (row + col in diagonalSet2) continue

        colSet.add(col)
        diagonalSet1.add(row - col)
        diagonalSet2.add(row + col)
        points.add(row to col)
        go()
		
        // 원복
        colSet.remove(col)
        diagonalSet1.remove(row - col)
        diagonalSet2.remove(row + col)
        points.removeLast()
    }
}

fun main() = with(System.`in`.bufferedReader()){
    n = readLine().toInt()
    go()
    println(cnt)
}